异度部落格

JVM 运行时数据区域示意图如下所示:

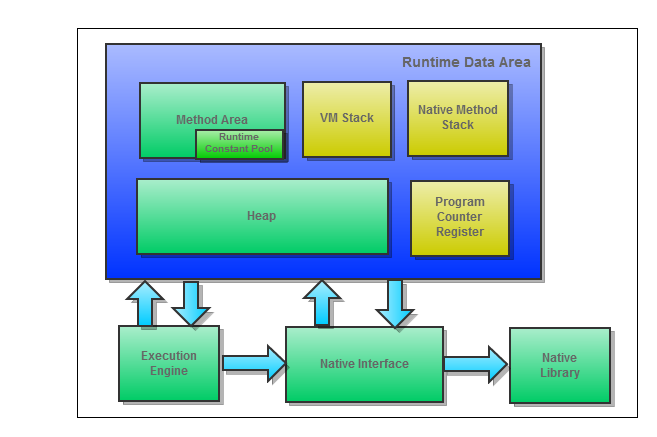
共享数据区域：Method Area、Heap
私有数据区域：VM Stack、Native Method Stack、Program Counter Register

1）方法区（Method Area）
    用于存储已被虚拟机加载的 class 信息、常量、静态变量、即时编译后的代码等数据。
    Exception：OutOfMemoryError

2）Java 虚拟机栈（JVM Stack）
    每个方法被执行时都会创建一个 Stack Frame 用于存储局部变量表、操作栈、动态链接、方法出口等信息。每个方法被调用直至执行完成，就对应着一个 Stack Frame 在虚拟机栈中从入栈到出栈的过程。
    Exception：StackOverflowError、OutOfMemoryError

3）本地方法区（Native Method）
    为使用 Native 方法服务的。
    Exception：StackOverflowError、OutOfMemoryError

4）Java 堆（Java Heap）
    JVM 中最大的一块区域。Java Heap 是被所有线程所共享，在 JVM 启动时创建。
    在 JVM 规范中的描述如下：The heap is the runtime data area from which memory for all class instances and arrays is allocated.

5）程序计数器（Program Counter Register）
    用于指示当前线程所执行的字节码行号指示器。
    Exception：None

6）运行时常量池（Runtime Constant Pool）
    是方法区的一部分。用于存放编译时生成的各种字面变量和常用符号
    Exception：OutOfMemoryError

OS: Ubunut 12.04

Hadoop: 1.0.4

JDK: OpenJDK 1.6

1.修改 hadoop/src/contrib/build-contrib.xml

在下面添加

<property name=”eclipse.home” location=”#{你的eclipse安装目录}” />
<property name=”version” value=”1.0.4″/>

2.修改 hadoop/src/contrib/eclipse-plugin/build.xml

1)添加

<path id=”hadoop-jars”>
<fileset dir=”${hadoop.root}/”>
<include name=”hadoop-*.jar”/>
</fileset>
</path>

2)在添加

<path id=”classpath”>
<pathelement location=”${build.classes}”/>
<pathelement location=”${hadoop.root}/build/classes”/>
<!– hadoop-core-1.0.4.jar dependency –>
<pathelement location=”${hadoop.root}”/>
<!– common lib dependency –>
<pathelement location=”${hadoop.root}/lib”/>
<path refid=”eclipse-sdk-jars”/>
<path refid=”hadoop-jars”/>
</path>

3)在添加

<target name=”jar” depends=”compile” unless=”skip.contrib”>
<mkdir dir=”${build.dir}/lib”/>
<!– 将以下jar包打进hadoop-eclipse-1.0.4.jar中 –>
<copy file=”${hadoop.root}/hadoop-core-1.0.4.jar” tofile=”${build.dir}/lib/hadoop-core.jar” verbose=”true”/>
<copy file=”${hadoop.root}/lib/commons-cli-1.2.jar” todir=”${build.dir}/lib” verbose=”true”/>
<copy file=”${hadoop.root}/lib/commons-lang-2.4.jar” todir=”${build.dir}/lib” verbose=”true”/>
<copy file=”${hadoop.root}/lib/commons-configuration-1.6.jar” todir=”${build.dir}/lib” verbose=”true”/>
<copy file=”${hadoop.root}/lib/jackson-mapper-asl-1.8.8.jar” todir=”${build.dir}/lib” verbose=”true”/>
<copy file=”${hadoop.root}/lib/jackson-core-asl-1.8.8.jar” todir=”${build.dir}/lib” verbose=”true”/>
<copy file=”${hadoop.root}/lib/commons-httpclient-3.0.1.jar” todir=”${build.dir}/lib” verbose=”true”/>
<jar
jarfile=”${build.dir}/hadoop-${name}-${version}.jar”
manifest=”${root}/META-INF/MANIFEST.MF”>
<fileset dir=”${build.dir}” includes=”classes/ lib/”/>
<fileset dir=”${root}” includes=”resources/ plugin.xml”/>
</jar>
</target>

3.将 hadoop-core-1.0.4.jar 复制到 hadoop/build 目录下

4.将 hadoop/lib/commons-cli-1.2.jar 复制到 hadoop/build/ivy/lib/Hadoop/common（没有请自行创建）目录下

5.进入 hadoop/src/contrib 目录，执行 ant jar

6.将 hadoop/build/contrib/eclipse-plugin/hadoop-eclipse-plugin-1.0.4.jar 复制到 eclipse/plugins 目录下

参考资料：

http://tianwenbo.iteye.com/blog/1464242 http://blog.csdn.net/yundixiaoduo/article/details/7451753 http://hi.baidu.com/geogrex/item/4e5853ce8fd4e01f0ad93a9f#0

OS: Ubuntu 12.04   Hadoop: Hadoop 1.0.4

1.安装集群所需软件

sudo apt-get install install ssh
sudo apt-get install rsync

配置ssh免密码登录

ssh-keygen -t dsa -P '' -f ~/.ssh/id_dsa
cat ~/.ssh/id_dsa.pub >>~/.ssh/authorized_keys

验证是否成功

ssh localhost

2.安装JDK

安装部分就不重复了，主要说明下环境变量的添加

sudo vi /etc/profile

将下面三句话添加到最后

export JAVA_HOME=/usr/lib/jvm/java-6-openjdk
export PATH=$JAVA_HOME/bin:$PATH
export CLASSPATH=.:$JAVA_HOME/lib/dt.jar:$JAVA_HOME/lib/tools.jar

3.安装Hadoop

下载地址：http://apache.etoak.com/hadoop/common/ 建议选择：1.0.x版本的tar文件，不建议使用deb或者rpm的包，因为后面回带来很复杂的程序权限问题。 修改配置文件，指定JDk安装路径

vi conf/hadoop-env.sh

export JAVA_HOME=/usr/lib/jvm/java-6-openjdk

修改Hadoop核心配置文件core-site.xml，这里配置的是HDFS的地址和端口号

vi conf/core-site.xml

<pre class="brush: xml; gutter: true; first-line: 1"><configuration>
     <property>
         <name>fs.default.name</name>
         <value>hdfs://localhost:9000</value>
     </property>
<property>
    <name>hadoop.tmp.dir</name>
    <value>/home/killua/Application/tmp/hadoop-${user.name}</value>
  </property>
</configuration>

修改Hadoop中HDFS的配置，配置的备份方式默认为3，因为安装的是单机版，所以需要改为1 vi conf/hdfs-site.xml

<configuration>
     <property>
         <name>dfs.replication</name>
         <value>1</value>
     </property>
</configuration>

修改Hadoop中MapReduce的配置文件，配置的是JobTracker的地址和端口

vi conf/mapred-site.xml

<configuration>
	<property>
		<name>mapred.job.tracker</name>
		<value>localhost:9001</value>
	</property>
  </configuration>

启动Hadoop，在启动之前，需要格式化Hadoop的文件系统HDFS

bin/hadoop namenode -format
然后启动Hadoop所有服务，输入命令

bin/start-all.sh

**4.验证是否安装成功**
打开浏览器，分别输入一下网址：
http://localhost:50030 (MapReduce的Web页面)
http://localhost:50070 (HDfS的web页面)

ICTCLAS（Institute of Computing Technology,Chinese Lexical Analysis System），由中国科学院计算技术研究开发，功能包括中文分词；词性标注；命名实体识别；新词识别；同时支持用户词典；支持繁体中文；支持 gb2312、GBK、UTF8 等多种编码格式，是世界上最好的汉语词法分析器之一。 下载地址：http://ictclas.org/ictclas_download.aspx

原系统只提供了 C++和 Java 版本，为了方便广大 Pythoner，决定用 python 对其进行重新封装。目前仅支持 Linux，Windows 版本开发中。 pyictclas 模块中包含三个类：一个 PyICTCLAS 类，用于分词工具的调用;一个是 CodeType?类，用于存放各种编码的枚举类型;一个是 POSMap 类用于存放标注集枚举类型。

项目主页：http://code.google.com/p/python-ictclas/

该项目废除，新项目参考：http://www.yidooo.net/archives/nlpir-python-version.html

【试题描述】写一个函数，求两个整数的和，要求在函数体内不得使用加减乘除四则运算符合。

【试题来源】未知

【参考代码】

int add(int num1, int num2) {

	int sum;
	int carry;
	do {
		sum = num1 ^ num2;
		carry = (num1 & num2) << 1;

		num1 = sum;
		num2 = carry;
	} while(num2 != 0);

	return num1;
}

【试题描述】我们把只包含因子2、3和5的数称作丑数。求按从到大的顺序的第1500个丑数。例如6,8是丑数，而14不是，因为它包含因子7.习惯上把1当作第一个丑数。

【试题来源】未知

【参考代码】

int Min(int a, int b, int c) {

	return (a < b ? a : b) < c ? (a < b ? a : b) : c;
}

int uglyNumber(int n) {

	if(n <= 0) {
		throw ("Invalid Input.");
	}

	long* uglyNum = new long[n];
	uglyNum[0] = 1;

	int index2 = 0;
	int index3 = 0;
	int index5 = 0;
	int indexLast = 0;

	while(indexLast < n) {
		int min = Min(uglyNum[index2] * 2, uglyNum[index3] * 3, uglyNum[index5] * 5);
		uglyNum[++indexLast] = min;

		while(uglyNum[index2] * 2 <= uglyNum[indexLast]) {
			index2++;
		}

		while(uglyNum[index3] * 3 <= uglyNum[indexLast]) {
			index3++;
		}

		while(uglyNum[index5] * 5 <= uglyNum[indexLast]) {
			index5++;
		}
	}

	return uglyNum[n - 1];

}

【试题描述】输入一个二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成的一条路径。

【试题来源】未知

【参考代码】

void findPath(BinaryTreeNode* rootNode, int expectSum,
		vector<int>& path, int curSum) {

	if(rootNode == NULL) {
		return ;
	}

	path.push_back(rootNode->value);
	curSum += rootNode->value;

	if(rootNode->left == NULL && rootNode->right == NULL
			&& curSum == expectSum) {
		cout << "Find a path: ";
		for(vector<int>::iterator iter = path.begin(); iter != path.end(); iter++) {
			cout << *iter << " ";
		}
		cout << endl;
	}

	if(rootNode->left != NULL) {
		findPath(rootNode->left, expectSum, path, curSum);
	}

	if(rootNode->right != NULL) {
		findPath(rootNode->right, expectSum, path, curSum);
	}

	path.pop_back();
	curSum -= rootNode->value;
}

void findPaths(BinaryTreeNode* rootNode, int expectSum) {

	vector<int> path;
	findPath(rootNode, expectSum, path, 0);
}

【试题描述】输入一棵二叉树的根结点，求该树的深度。从根结点到叶子结点依次经过的结点（含根、叶子节点）形成树的一条路径，最长路径的长度为树的深度。

【试题来源】未知

【参考代码】

int treeDepth(BinaryTreeNode* rootNode) {

	if(rootNode == NULL) {
		return 0;
	}

	int leftSubTreeDepth = treeDepth(rootNode->left);
	int rightSubTreeDepth = treeDepth(rootNode->right);

	return leftSubTreeDepth > rightSubTreeDepth ? (leftSubTreeDepth + 1) : (rightSubTreeDepth + 1);
}

【试题描述】输入一个字符串，打印出该字符串中字符的所有排列。例如输入字符串abc，则打印出a，b，c所能排列出来的所有字符串abc，acb，bac，bca，cab，cba。

【试题来源】未知

【参考代码】

#include <iostream>
#include <cstring>
#include<cstdio>
#include<cstdlib>
using namespace std;

void permutation(char* str, int begin) {

	if(begin == strlen(str)) {
		cout << str << endl;
	} else {
		for(int i = begin; i < strlen(str); ++i) {
			char tmp = str[i];
			str[i] = str[begin];
			str[begin] = tmp;

			permutation(str, begin + 1);

			tmp = str[i];
			str[i] = str[begin];
			str[begin] = tmp;
		}
	}
}

void permutation(char* str) {
	if(str == NULL) {
		return ;
	}

	permutation(str, 0);
}

int main() {
	char str[] = "abc";
	//char* str = "abc"; //Runtime Error
	permutation(const_cast<char*>(str));
	return 0;
}