引言
QLoRA（Quantized Low-Rank Adapter）是一种高效的微调方法，是 LoRA
的量化版本（什么是
LoRA？）。该调优方法由华盛顿大学发表于论文《QLORA: Efficient Finetuning of
Quantized LLMs》。通过降低内存使用，实现在单个 GPU
上对大型语言模型进行微调。它可以在单个 48GB GPU 上微调 650
亿个参数的模型，并且能够保持完整的 1 6 位微调任务性能。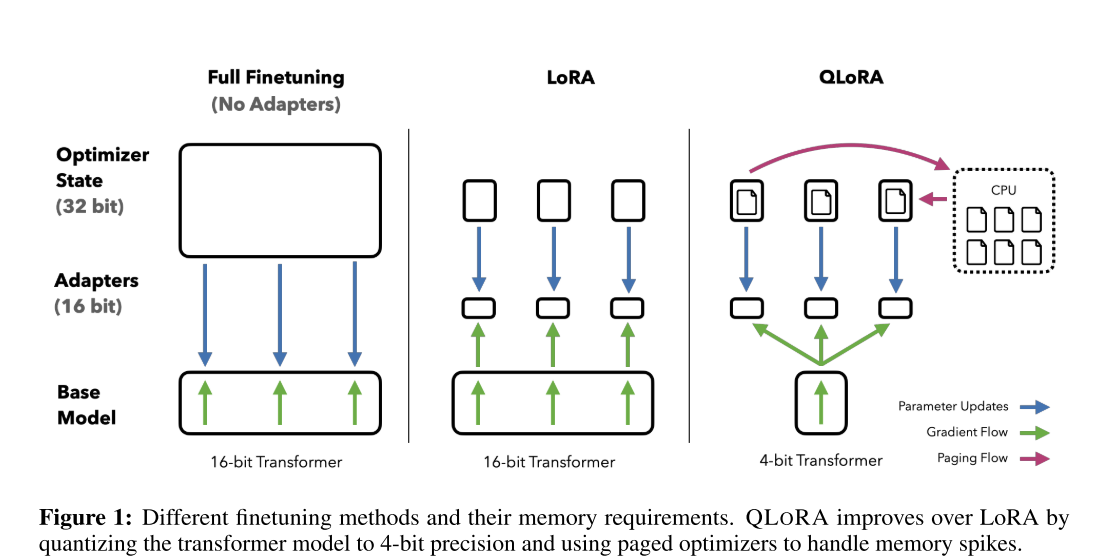 
基础技术介绍
Block-wise k-bit Quantization
量化指的是将连续或高精度的数值转换为较低精度（比如较少的位数）的表示形式的过程。这通常用于减少模型的存储需求和加快其运算速度。例如，将一个 FP32 的 tensor 转成 Int8: \[X^{\text{Int8}} = \text{round}\left(\frac{127}{\text{absmax}(X^{\text{FP32}})} \cdot X^{\text{FP32}}\right)=round(c^{\text{FP32}})\] 其中，c 为量化常数。逆量化公式则为： \[\text{dequant}(c^{\text{FP32}}, X^{\text{Int8}}) = \frac{X^{\text{Int8}}}{c^{\text{FP32}}}\] 这种常规的量化方法的局限性也非常明显，当 tensor 中有一个非常大的数字（一般称为 outlier）时，将影响最终的量化结果。
因此，Block-wise k-bit Quantization 方法就是把 tensor 线性平展开，然后分割成 B 段，每段有自己的量化常数 c，独自量化。
Low-rank Adapters
LoRA，全称为“Low-Rank Adaptation”，尤其是在大型预训练语言模型（比如 GPT-3）的微调领域中。它是一种参数高效的模型微调技术，通过引入低秩的权重矩阵来修改预训练模型的自注意力机制。
在大型语言模型的背景下，LoRA 的关键优势是它能够在增加极少量参数的情况下，有效地适应新的任务或数据集。这一点尤其重要，因为全面重新训练这些大型模型需要大量的计算资源，而 LoRA 提供了一种更为节能的替代方案。
具体来说，LoRA 的工作原理是在自注意力模块的键（key）和值（value）矩阵中引入低秩矩阵。这些低秩矩阵与原始的键值对进行相乘，产生新的键值对，用于微调模型。因为这些矩阵的秩很低，所以新增加的参数数量较少，但这些参数的引入足以让模型学习到新任务的特定特征。
LoRA 的这种设计旨在保持预训练模型的大部分权重不变，同时仅对模型进行必要的小规模修改，从而快速适应新的任务。这样的方法在保持模型性能的同时，还能显著减少部署和运行大型模型所需的资源。
PEFT
PEFT（Parameter- Efficient Finetune）是一种在自然语言处理（NLP）中常用的方法，特别是在大型预训练语言模型的微调阶段。PEFT 方法的关键思想是，在保持大部分预训练模型参数固定不变的同时，只微调一小部分参数。这些参数可以是添加到模型的新参数，也可以是模型内部的一小部分可训练参数。这样做的好处是显著减少了微调过程中的内存和计算需求，同时仍然保持了模型的表现力。
核心技术
4 bit Normal Quantization
论文中提出的 4-bit NormlFLoat 量化是对 Quantile Quantization(分位量化)进行了改进，并结合上诉 Block-wise Quantization，降低计算复杂度和误差。
以 4-bit 量化为例，参数将被映射到 16 个可能的值（从 0 到 15）中的某一个，类似于四舍五入的方式。然而，这种传统量化方法的一个主要缺点是，量化后的参数分布可能与原始分布相差甚远。比如，如果有一个极大的值，那么大多数参数可能都会被量化到 0，从而导致模型性能显著下降。
为了解决这一问题，作者采用了分位量化（Quantile Quantization）方法。那么，分位量化是什么呢？仍然以 4-bit 量化为例，这意味着有 16 个不同的值可以选择。在分位量化中，首先将输入参数按大小排序（Quantile），然后将它们等分成 16 份（Block-Wise），每份对应一个量化值。这种方法在量化过程中能够更好地保持参数的原始分布，从而在降低参数精度的同时，尽可能减少对模型性能的影响。
上述分位量化会额外引入明显的计算开销，因为每次有参数输入进来都需要对齐进行排序并等分。
作者发现预训练的参数基本上都服从均值为 0 的正态分布，可以将其缩放到[-1,
1]的范围中。同时可以将正态分布 N(0,1)划分为 2^k+1 份，并缩放到[-1,
1]的范围中。这样就能直接将参数映射到对应的分位，不用每次都对参数进行排序。
但是这样做饭也会有一个缺点，参数 0 量化后可能不在 0
的位置上了，就没法表达 0
的特殊意义了。为此作者还做了一点改进，即分别将负数和整数部分划分为 2^k-1
份，参数 0 还是放在 0 原本的位置上。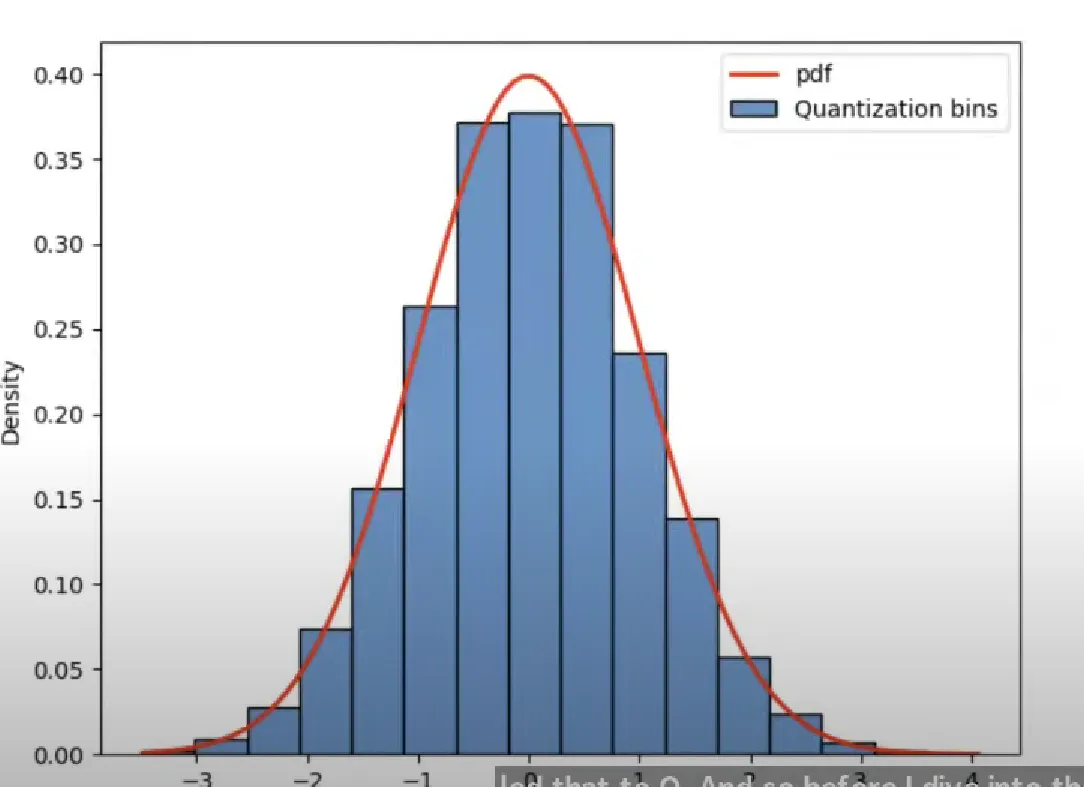 
Double Quantization
分块量化中每个 block 都会额外产生一个量化常数 c。以量化 32bit
参数、block 大小 64 为例，每个 block 会引入 32bit
的量化常数，对应每个参数会额外引入 32/64=0.5bit 的额外开销。
论文采用了双重量化方法，如下图所示：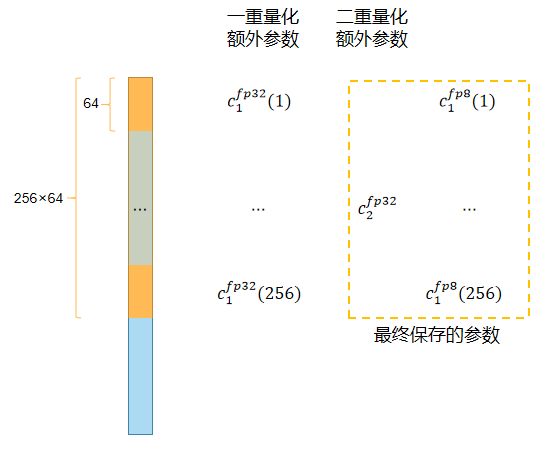 
在第一次量化后，并不会直接储存量化常数 c1，而是按照 block 大小 256
对量化常数再量化到 8bit 上去储存，这个阶段会再引入一个量化常数
c2。最终保存的额外参数为 8/64 + 32/(64 ·
256)=0.127bits，也就是每个参数减少 0.5-0.127=0.373bits
Paged Optimizers
Paged Optimizer 将优化器需要存储的数据（例如权重和梯度）分成多个小块或“页”。在每个训练步骤中，只加载当前需要的数据页到内存中，而不是一次性将所有数据加载进内存。这种方法允许在相对较小的内存中有效地处理大型模型，因为任何时候都只有部分数据被加载。
QLoRA 训练
所以 QLoRA 最终训练的表达为：
\[ Y^{\text{BF16}} = X^{\text{BF16}} \text{doubleDequant}\left(c_{1}^{\text{FP32}}, c_{2}^{\text{k-bit}}, W^{\text{NF4}}\right) + X^{\text{BF16}}{L_1}^{\text{BF16}}{L_2}^{\text{BF16}} \]
其中：
\[ \text{dequant}\left(c_1^{\text{FP32}},c_2^{\text{FP32}}, W^{\text{k-bit}}\right) = dequant(dequant(c_1^{FP32}, c_2^{k-bit}), W^{NF4})=W^{BF16} \]