概述
在传统的自注意力机制中,注意力矩阵的计算复杂度为 O(N²),其中 N 是序列的长度。对于长序列的输入(如文本或图像中的像素点),这种计算代价极高,特别是在训练大型语言模型或视觉模型时,内存占用和计算开销随着序列长度的增加而急剧上升。此外,注意力矩阵的大小为 N×N,这也对 GPU 内存消耗极大。自注意力机制不仅在计算时消耗大量内存,还需要存储所有中间变量(如 Q、K、V 矩阵及注意力权重),以支持后续的反向传播。
因此,找到有效降低 Transformer 模型 O(N²) 复杂度的方案至关重要。理想情况下,若能将复杂度降至 O(N),将大大提升模型效率。即使无法完全实现 O(N),逼近这一复杂度也是十分有价值的。在这一背景下,Flash Attention 应运而生,成为解决该问题的有效方案。
从 Flash Attention(Fast and Memory Efficient Exact Attention with IO-Awareness)的命名可见其优势:
- Fast(with IO-Awareness):计算速度快,与以往通过减少 FLOPs(浮点运算次数)的方法不同,Flash Attention 发现性能瓶颈不在计算,而在显存的访问(后文将对此详细分析)。
- Memory Efficient:在 Flash Attention 中,内存使用压力从 O(N²) 降至 O(N),显著节省内存。
- Exact Attention:与稀疏 Attention 不同,Flash Attention 完全等效于标准 Attention。
背景知识
计算限制与内存限制
首先介绍几个关键概念:
- \(π\):硬件计算能力上限,表示一个计算平台在全负荷情况下每秒能够执行的浮点运算次数,单位为 FLOPS(浮点运算次数每秒)。
- \(β\):硬件带宽上限,表示一个计算平台在全负荷情况下每秒能够完成的数据交换量,单位为 Byte/s。
- \(π_t\):某算法所需的总运算量,单位为 FLOPs。
- \(β_t\):某算法所需的总数据读取和存储量,单位为 Byte。
在实际执行过程中,时间不仅消耗在计算上,也消耗在数据读取和存储上。因此,我们定义:
- \(T_{cal}\):算法执行所需的计算时间,其公式为 \(T_{cal} = π_t / π\)。
- \(T_{load}\):算法执行所需的数据读取与存储时间,公式为 \(T_{load} = β_t / β\)。
由于计算和数据传输可以同时进行,我们定义算法的总执行时间:
- T:算法的总执行时间,其公式为 \(T = max(T_{cal}, T_{load})\)。
简而言之,算法的总运行时间由计算时间和数据读取时间中较大的值决定。
- 当 \(T_{cal} > T_{load}\) 时,算法的瓶颈在计算部分,称为计算限制(math-bound)。此时,\(π_t/π > β_t/β\),即 \(π_t/β_t > π/β\)。
- 当 \(T_{cal} < T_{load}\) 时,瓶颈在数据读取部分,称为内存限制(memory-bound)。此时,\(π_t/π < β_t/β\),即 \(π_t/β_t < π/β\)。
算法的计算强度(Operational Intensity)定义为 \(π_t/β_t\)。
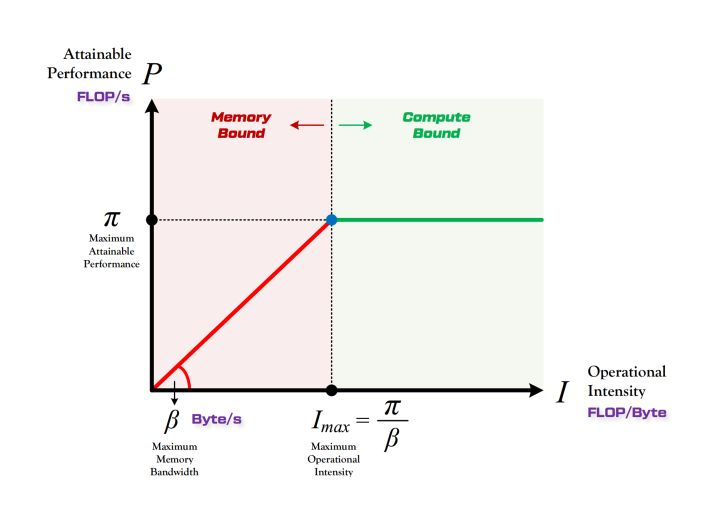
对于一个运算量为 \(π_t\),数据读取存储量为 \(β_t\) 的算法,其在算力上限为 \(π\) 和带宽上限为 \(β\) 的硬件上,能达到的最大性能 P(即每秒最多可达的浮点运算次数)是多少?
Roofline 模型为解答这一问题而提出。它能直观展示算法在硬件上的运行速度,如下图所示。
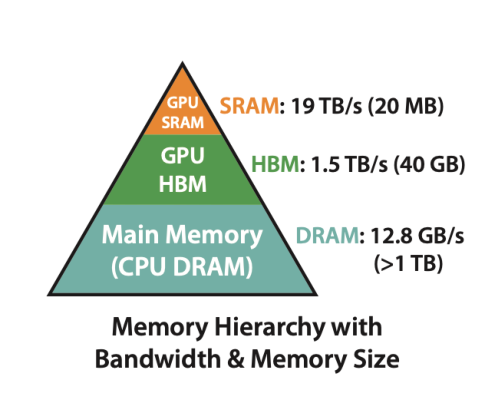
GPU 存储与计算
GPU 存储分类
通常,GPU 存储分为片上内存(on-chip memory)和片下内存(off-chip memory),这主要取决于存储单元是否位于芯片内部。
- 片上内存:用于缓存等,容量小但带宽极高。如上图中的 SRAM,容量仅 20MB,带宽却达 19TB/s。
- 片下内存:用于全局存储(即显存),容量大但带宽相对较小。如 HBM,容量可达 40GB,带宽为 1.5TB/s。
GPU 的计算
GPU 的计算流程可以理解为:数据从显存(HBM)加载到片上内存(SRAM),由 SM(Streaming Multiprocessor)读取并进行计算,计算结果再通过 SRAM 返回显存。具体可参考:NVIDIA GPU 原理详解。
显存带宽远低于 SRAM,因此从显存读取数据往往较耗时。为了优化读取效率,我们会尽量将数据填满 SRAM,从而减少频繁读取。
Kernel 融合
为减少显存读取次数,若 SRAM 容量允许,多个计算步骤可合并在一次数据加载中完成。这被称为kernel 融合。
Attention 计算
自注意力机制的计算复杂度为 O(N²),在长序列上,这往往是 Transformer 的主要计算瓶颈。具体计算过程可参考:Transformer 101。
FlashAttention 的核心思路
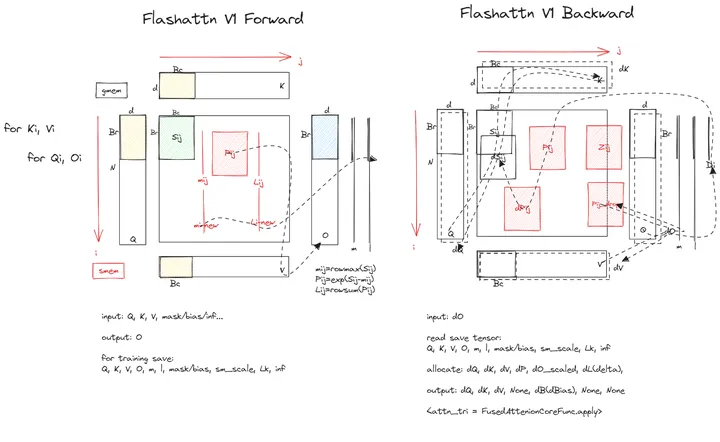
Flash Attention 出自论文 《FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness》,其核心在于通过分块避免存储大规模注意力矩阵(N×N)。算法主要分为两个步骤:
- 分块计算:将输入矩阵划分为小块,并逐块在 SRAM 上计算注意力,避免将整个 N×N 矩阵存储于显存。
- 重计算:通过前向传播时保存归一化因子,避免在反向传播中存储中间结果,而是通过重计算得出注意力矩阵。这虽然增加了浮点运算次数,但通过减少 HBM 访问,提升了整体效率。

在实现上,FlashAttention 使用 Kernel Fusion 将矩阵乘法、softmax 归一化、masking 和 dropout 操作合并为一次内存读取后在 SRAM 中完成,减少对显存的读写操作,提升了执行效率。
计算量分析
标准 Attention
标准自注意力的计算复杂度为 \(O(N²d)\),主要由矩阵乘法组成。由于需要计算并存储 N×N 的注意力矩阵,计算量和存储需求随序列长度平方增长。
FlashAttention
FlashAttention 保持相同的计算量,但通过分块和重计算减少了显存使用。实验表明,尽管重计算增加了操作次数,FlashAttention 比标准 Attention 快 7.6 倍。
显存需求分析
标准 Attention
标准 Attention 的显存需求为 O(N²),在长序列下,存储注意力矩阵的成本非常高。
FlashAttention
FlashAttention 将显存需求降低到 O(N),通过分块处理和重计算,显著减少了显存使用。实验显示,其显存消耗可减少至标准 Attention 的 1/20。
IO 复杂度分析
标准 Attention
标准 Attention 的 IO 复杂度为 O(N²),需要频繁读写大规模矩阵。
FlashAttention
FlashAttention 的 IO 复杂度为 O(N²d²/M),通过减少从 HBM 到 SRAM 的数据传输,IO 开销显著降低,比标准 Attention 少 9 倍访问。
复杂度总结
| 对比维度 | 标准 Attention | FlashAttention |
|---|---|---|
| 计算量 | \(O(N²d)\),随序列长度平方增长 | \(O(N²d)\),通过重计算优化速度 |
| 显存需求 | \(O(N²)\),存储 N×N 注意力矩阵 | \(O(N)\),分块和重计算显著降低显存需求 |
| IO 复杂度 | \(O(N²)\),频繁 HBM 访问 | \(O(N²d² / M)\),减少 HBM 到 SRAM 的读写操作 |
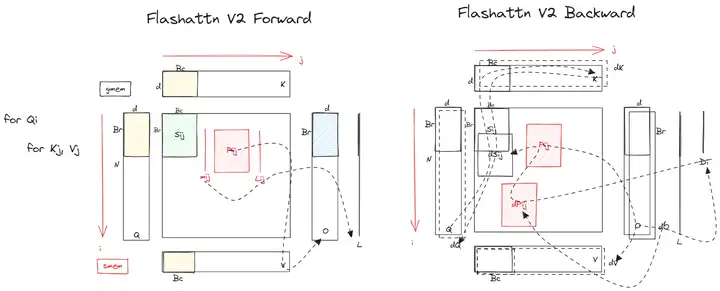
FlashAttention V2 的改进点
FlashAttention V2 出自论文《FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning》,主要改进包括:
- 优化计算次序,减少非矩阵计算量。
- 增加 seq_len 维度的并行计算,提升 SM 利用率。
- 优化 warp 级工作模式,减少内部通信和 shared memory 访问。
FlashAttention V3 的改进点
Flash Attention V3 出自论文《FlashAttention-3: Fast and Accurate Attention with Asynchrony and Low-precision》,主要改进如下:
- 引入生产者-消费者异步机制,提升并行度。
- 优化 GEMM 和 Softmax 操作的重叠计算。
- 支持 FP8 低精度硬件加速,提升吞吐量并减少精度损失。